Ce chapitre est un complément sur les espaces topologiques et les semi-normes, on va étudier les espaces vectoriels topologiques, ces espaces sont une des structures de base de l'analyse fonctionnelle. Ce sont des espaces munis d'une structure topologique associée à une structure d'espace vectoriel, avec des relations de compatibilité entre les deux structures. Ensuite on étudie les semi-normes, car la topologie induite par la semi-norme confère à l'espace une structure d'espace vectoriel topologique.
- Teacher: Hamid Khiar

Ce cours à l'objectif ambitieux de permettre aux étudiants d'appréhender le Latex sans difficulté, il présente ce qu'il faut savoir maîtriser dans la rédaction et la présentation d'un document de recherche scientifique.
- Teacher: Fatima Boukhalfa
et d'apprendre de nouvelles méthodes de résolution des problèmes de cauchy ainsi l'utilisation de la fonction de Green et aussi étudier un problème de Struim Liuoville
- Teacher: Imane MAMMAR
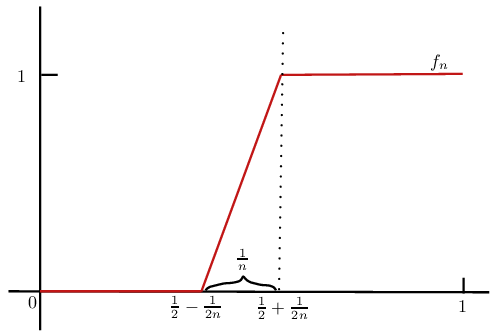
Cette matière permet à l'étudiant d'approfondir ses connaissances en topologie et de cerner les opérateurs linéaires sur les espaces de Hilbert.
- Teacher: Fatima Zahra TCHOUAR